Elektrik Mühendisliğinde dirençleri, akımları veya DC voltajlarını bir araya getirmek için kullanılan matematik, tam sayılar veya kesirler olarak kullanılan “gerçek sayılar” olarak adlandırılanları kullanır.
Ancak, özellikle frekansa bağlı sinüzoidal kaynaklar ve vektörlerle uğraşırken kullanmamız gereken tek sayı türü gerçek sayılar değildir. Normal veya gerçek sayıları kullanmanın yanı sıra, karmaşık denklemlerin negatif sayıların karekökü olan sayılarla çözülmesine izin vermek için Karmaşık Sayılar tanıtıldı, √ -1 .
Elektrik mühendisliğinde bu tür bir sayıya “hayali sayı” denir ve sanal bir sayıyı gerçek bir sayıdan ayırt etmek için elektrik mühendisliğinde yaygın olarak j-operatörü olarak bilinen ” j ” harfi kullanılır. Böylece “ j ” harfi , onun hayali sayı işlemini belirtmek için gerçek bir sayının önüne yerleştirilir.
Hayali sayılara örnekler: j3 , j12 , j100 vb. O halde bir karmaşık sayı iki farklı fakat birbiriyle çok ilişkili kısımdan oluşur, bir “Gerçek Sayı” artı bir “Hayali Sayı”.
Karmaşık Sayılar , iki farklı eksene referans verilen iki boyutlu bir kompleks veya s-düzlemindeki noktaları temsil eder. Yatay eksene “gerçek eksen”, dikey eksene “hayali eksen” denir. Bir karmaşık sayının reel ve sanal kısımları sırasıyla Re(z) ve Im(z) olarak kısaltılır.
Gerçek (aktif bileşen) ve hayali (reaktif bileşen) sayılardan oluşan karmaşık sayılar, DC Devrelerini analiz etmek için kullanılan temel cebir ile tamamen aynı şekilde toplanabilir, çıkarılabilir ve kullanılabilir .
Matematikte hayali sayıların toplanması veya çıkarılması için kullanılan kurallar ve yasalar, gerçek sayılarla aynıdır, j2 + j4 = j6 vb. Tek fark çarpmadadır, çünkü iki hayali sayı birlikte çarpıldığında negatif bir gerçek sayı olur. Gerçek sayılar aynı zamanda karmaşık bir sayı olarak da düşünülebilir, ancak j0 olarak etiketlenmiş sıfır hayali bir kısmı vardır.
j-operatörü √ -1 değerine tam olarak eşit bir değere sahiptir , bu nedenle “ j “, ( j x j ) ‘ nin art arda çarpması j’nin aşağıdaki -1 , -j ve +1 değerlerine sahip olmasına neden olur . j-operatörü bir vektörün saat yönünün tersine dönüşünü belirtmek için yaygın olarak kullanıldığından, “ j “, j 2 , j 3 vb.’nin her art arda çarpması veya kuvveti, vektörü saat yönünün tersine 90 o’luk sabit bir açıyla dönmeye zorlayacaktır. aşağıda gösterildiği gibi yön. Benzer şekilde, vektörün çarpımı a -j ile sonuçlanırsaOperatör, daha sonra faz kayması -90 o olacaktır , yani saat yönünde bir dönüş.
j-operatörünün vektör dönüşü

Dolayısıyla, hayali bir sayıyı j 2 ile çarpmak vektörü saat yönünün tersine 180 o döndürür, j 3 ile çarpmak onu 270 o döndürür ve j 4 ile 360 o döndürür veya orijinal konumuna geri döndürür. j 10 veya j 30 ile çarpma , vektörün uygun miktarda saat yönünün tersine dönmesine neden olur. Birbirini izleyen her dönüşte, vektörün büyüklüğü her zaman aynı kalır.
Elektrik Mühendisliğinde karmaşık bir sayıyı grafik veya matematiksel olarak göstermenin farklı yolları vardır. Kosinüs ve sinüs kuralını kullanan böyle bir yol, Kartezyen veya Dikdörtgen Form olarak adlandırılır .
Dikdörtgen Formu Kullanan Karmaşık Sayılar
Fazörler hakkındaki son öğreticide , karmaşık bir sayının, genelleştirilmiş biçimini alan bir reel kısım ve bir sanal kısım ile temsil edildiğini gördük:

- Neresi:
- Z – Vektörü temsil eden Karmaşık Sayıdır
- x – Gerçek kısım veya Aktif bileşendir
- y – Hayali kısım veya Reaktif bileşendir
- j – √ -1 ile tanımlanır
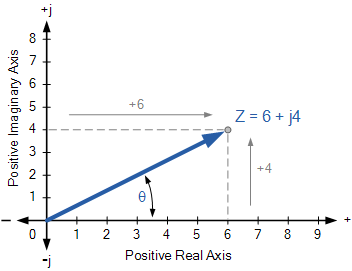
Dikdörtgen biçiminde, karmaşık bir sayı, karmaşık veya s-düzlemi olarak adlandırılan iki boyutlu bir düzlemde bir nokta olarak temsil edilebilir . Örneğin, Z = 6 + j4 , gösterildiği gibi koordinatları yatay gerçek eksende 6 ve dikey hayali eksende 4’ü temsil eden tek bir noktayı temsil eder.
Karmaşık veya s-düzlemini kullanan Karmaşık Sayılar
Ancak dikdörtgen biçimindeki bir karmaşık sayının hem reel hem de sanal kısımları pozitif veya negatif bir sayı olabileceğinden, hem reel hem de sanal eksen hem pozitif hem de negatif yönlerde uzanmalıdır. Bu daha sonra aşağıda gösterildiği gibi Argand Diyagramı adı verilen dört kadranlı karmaşık bir düzlem üretir.
Dört Çeyrek Argand Diyagramı

Argand diyagramında yatay eksen, dikey sanal eksenin sağındaki tüm pozitif gerçek sayıları ve dikey sanal eksenin solundaki tüm negatif gerçek sayıları temsil eder. Tüm pozitif sanal sayılar yatay eksenin üzerinde gösterilirken tüm negatif sanal sayılar yatay gerçek eksenin altındadır. Bu daha sonra QI , QII , QIII ve QIV olarak etiketlenmiş dört farklı kadranlı iki boyutlu bir karmaşık düzlem üretir .
Yukarıdaki Argand diyagramı, yarıçapı fazörün büyüklüğü tarafından verilen karmaşık düzlemde bir nokta olarak dönen bir fazörü temsil etmek için de kullanılabilir, her 2π/ω saniyede bir tam daire çizecektir.
Daha sonra, 90 o’luk dönüşler için hem kutupsal hem de dikdörtgen biçimde karmaşık bir sayının tanımını göstermek için bu fikri daha da genişletebiliriz.

Karmaşık Sayılar ayrıca Z = 6 + j0 veya Z = 0 + j4 gibi “sıfır” gerçek veya sanal kısımlara sahip olabilir . Bu durumda noktalar doğrudan gerçek veya hayali eksene çizilir. Ayrıca, karmaşık bir sayının açısı, dik açılı üçgenlerin açılarını hesaplamak için basit trigonometri kullanılarak hesaplanabilir veya pozitif gerçek eksenden başlayarak Argand diyagramı etrafında saat yönünün tersine ölçülebilir.
O zaman 0 ile 90 o arasındaki açılar birinci kadranda ( I ), açılar ( θ ) ikinci kadranda ( II ) 90 ile 180 o arasında olacaktır . Üçüncü kadran ( III ) 180 ile 270 o arasındaki açıları içerirken , tam daireyi tamamlayan dördüncü ve son kadran ( IV ) 270 ile 360 o arasındaki açıları içerir vb. Dört kadranda da ilgili açılar şuradan bulunabilir:
tan -1 (hayali bileşen ÷ gerçek bileşen)
Karmaşık Sayılarda Toplama ve Çıkarma
Karmaşık sayıların toplanması veya çıkarılması, matematiksel veya grafiksel olarak dikdörtgen biçiminde yapılabilir. Toplama için, önce reel kısımlar toplamın gerçel kısmını oluşturacak şekilde bir araya getirilir, ardından sanal kısımlar toplamın sanal kısmını oluşturacak şekilde toplanır ve bu işlem örnek olarak iki karmaşık sayı A ve B kullanılarak aşağıdaki gibidir .
Karmaşık Toplama ve Çıkarma

Karmaşık Sayılar Örnek No1
İki vektör sırasıyla A = 4 + j1 ve B = 2 + j3 olarak tanımlanır. İki vektörün hem dikdörtgen ( a + jb ) biçiminde hem de Argand Diyagramı olarak grafiksel olarak toplamını ve farkını belirleyin .
Matematiksel Toplama ve Çıkarma
Ekleme

Çıkarma
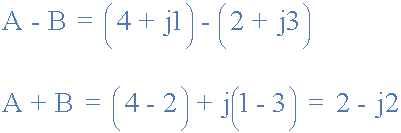
Grafik Toplama ve Çıkarma

Karmaşık Sayılarda Çarpma ve Bölme
Karmaşık sayıların dikdörtgen biçiminde çarpımı, j-operatörünün ardışık çarpımı için bazı ek kurallarla birlikte, normal cebir ile aşağı yukarı aynı kuralları takip eder, burada: j 2 = -1 .
Örneğin, yukarıdan A = 4 + j1 ve B = 2 + j3 vektörlerimizi çarparsak bize aşağıdaki sonucu verir.

Matematiksel olarak, karmaşık sayıların dikdörtgen biçiminde bölünmesi, denklemin paydasını gerçek bir sayıya dönüştürmek için payda eşlenik işlevinin kullanılmasını gerektirdiğinden gerçekleştirmek biraz daha zordur. Buna “rasyonelleştirme” denir. Daha sonra karmaşık sayıların bölünmesi en iyi şekilde daha sonra inceleyeceğimiz “Kutup Biçimi” kullanılarak gerçekleştirilir. Ancak, dikdörtgen biçiminde bir örnek olarak, A vektörünün değerini B vektörüne bölünerek bulalım.
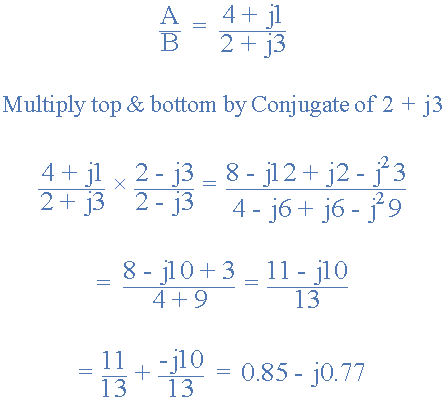
Karmaşık Eşlenik
Karmaşık eşleniği veya basitçe bir karmaşık sayının eşleniği , gerçek sayının cebirsel işareti aynı tutularak karmaşık sayıların cebirsel işaretinin tersine çevrilmesiyle bulunur ve z’nin karmaşık eşleniğini tanımlamak için z sembolü kullanılır . Örneğin, z = 6 + j4’ün eşleniği z = 6 – j4’tür , aynı şekilde z = 6 – j4’ün eşleniği de z = 6 + j4’tür .
Karmaşık bir eşlenik için Argand diyagramındaki noktalar, gerçek eksende orijinal karmaşık sayı ile aynı yatay konuma sahiptir, ancak dikey konumlara zıttır. Böylece karmaşık eşlenikler, karmaşık bir sayının yansıması olarak düşünülebilir. Aşağıdaki örnek, karmaşık bir sayı olan 6 + j4’ü ve karmaşık düzlemdeki eşleniğini göstermektedir.
Eşlenik Karmaşık Sayılar
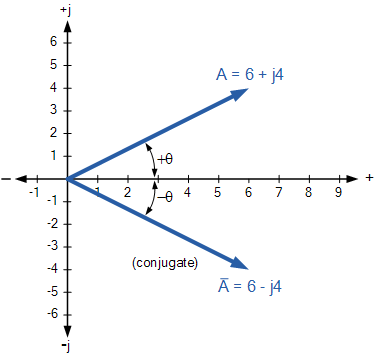
Bir karmaşık sayının ve onun karmaşık eşleniğinin toplamı yukarıda gördüğümüz gibi her zaman gerçek bir sayı olacaktır. Daha sonra karmaşık bir sayının ve onun eşleniğinin eklenmesi sonucu yalnızca gerçek sayı veya etkin bileşen olarak verirken, bunların çıkarılması yalnızca sanal bir sayı veya yalnızca reaktif bileşen verir. Karmaşık bir sayının eşleniği, bir AC devresinin dikdörtgen biçimini kullanarak görünen gücünü belirlemek için Elektrik Mühendisliğinde kullanılan önemli bir unsurdur.
Kutup Formu Kullanan Karmaşık Sayılar
Noktaları karmaşık düzlemde çizen dikdörtgen biçiminden farklı olarak , bir karmaşık sayının Kutup Biçimi , büyüklüğü ve açısı cinsinden yazılır. Böylece, bir kutupsal biçim vektörü şu şekilde sunulur: Z = A ∠±θ , burada: Z kutupsal biçimdeki karmaşık sayıdır, A vektörün büyüklüğü veya modulodur ve θ , A’nın açısı veya argümanıdır ; olumlu veya olumsuz. Noktanın büyüklüğü ve açısı yukarıdaki dikdörtgen formdakiyle aynı kalır, bu sefer kutupsal formda noktanın konumu aşağıda gösterildiği gibi “üçgen formda” temsil edilir.
Bir Karmaşık Sayının Kutup Biçimli Gösterimi

Bir noktanın kutupsal temsili üçgen biçimine dayandığından, karmaşık sayının hem büyüklüğünü hem de açısını bulmak için üçgenin basit geometrisini ve özellikle trigonometriyi ve Pisagor Teoremi’ni üçgenler üzerinde kullanabiliriz. Okuldan hatırladığımız gibi, trigonometri, kenarlar ve üçgenlerin açıları arasındaki ilişkiyle ilgilenir, böylece kenarlar arasındaki ilişkileri şu şekilde tanımlayabiliriz:
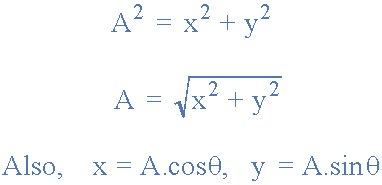
Yine trigonometri kullanılarak A’nın θ açısı aşağıdaki gibi verilir.

Sonra Kutupsal formda A’nın uzunluğu ve açısı bir nokta yerine karmaşık sayıyı temsil eder. Ayrıca kutupsal formda, karmaşık sayının eşleniği aynı büyüklüğe veya modüle sahiptir, değişen açının işaretidir, bu nedenle örneğin 6 ∠30 o’nun eşleniği 6 ∠– 30 o olacaktır .
Dikdörtgen Form ve Polar Form arasında dönüştürme
Dikdörtgen formda, bir vektörü dikdörtgen koordinatları cinsinden ifade edebiliriz; yatay eksen gerçek ekseni ve dikey eksen hayali ekseni veya j bileşenidir. Kutup biçiminde bu gerçek ve sanal eksenler basitçe “ A ∠θ ” ile temsil edilir. Daha sonra yukarıdaki örneğimizi kullanarak, dikdörtgen form ile kutupsal form arasındaki ilişki olarak tanımlanabilir.
Polar Formu Dikdörtgen Forma Dönüştürme, ( P→R )
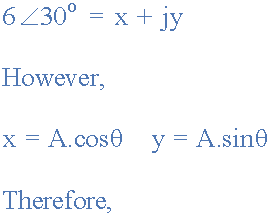

Dikdörtgen formdan kutupsal forma da aşağıdaki gibi dönebiliriz.
Dikdörtgen Formu Polar Forma Dönüştürme, ( R→P )

Kutup Formu Çarpma ve Bölme
Dikdörtgen biçim, yukarıda gördüğümüz gibi karmaşık sayıları toplamak ve çıkarmak için en iyisidir, ancak kutupsal biçim genellikle çarpma ve bölme için daha iyidir. İki vektörü kutupsal biçimde çarpmak için, önce iki modülü veya büyüklüğü birlikte çarpmamız ve sonra açılarını toplamamız gerekir.
Kutup Biçiminde Çarpma

6 ∠30 o ve 8 ∠– 45 o kutupsal formda çarpılması bize verir.
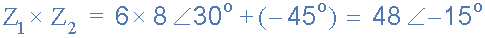
Kutup Biçiminde Bölme
Benzer şekilde, iki vektörü kutupsal biçimde birbirine bölmek için, iki modülü bölmeli ve ardından gösterildiği gibi açılarını çıkarmalıyız.

Neyse ki günümüzün modern bilimsel hesap makineleri, dikdörtgenin kutupsal forma ( R → P ) ve kutuptan dikdörtgen forma ( R → P ) kolayca dönüştürülmesine izin veren matematiksel fonksiyonlara (kitabınızı kontrol edin) sahiptir.
Üstel Form Kullanan Karmaşık Sayılar
Buraya kadar karmaşık sayıları Dikdörtgen Formda ( a+jb ) ve Kutup Formunda ( A ∠±θ ) düşündük. Ancak, sinüzoidin uzunluğuna (büyüklüğüne) ve faz açısına karşılık gelen, ancak doğal logaritmanın tabanını kullanan kutupsal forma benzer bir karmaşık sayıyı temsil etmek için üçüncü bir yöntem de vardır, e = 2.718 281.. bulmak için . karmaşık sayının değeri. Bu üçüncü yönteme Üstel Form adı verilir .
Üstel Form , karmaşık üstel olanı karmaşık düzlemde dönen bir nokta olarak tanımlamak için dik açılı bir üçgenin hem sinüs ( sin ) hem de kosinüs ( cos ) değerlerinin trigonometrik fonksiyonlarını kullanır. Noktanın konumunu bulmak için üstel form , adını İsviçreli matematikçi Leonhard Euler’den alan Euler’in Kimliğine dayanır ve şu şekilde verilir:

Daha sonra Euler’in kimliği, karmaşık düzlemde aşağıdaki dönen fazör diyagramı ile temsil edilebilir.

Euler kimliğinin yukarıdaki kutupsal forma çok benzediğini ve A e jθ gibi 1 büyüklüğüne sahip bir sayının da karmaşık bir sayı olduğunu bize gösterdiğini görebiliriz. 2 e j30 = 2∠30 , 10 e j120 = 10∠120 veya -6 e j90 = -6∠90 gibi üstel formdaki karmaşık sayıları kolayca kutupsal forma dönüştürmekle kalmaz , aynı zamanda Euler özdeşliği de verir. karmaşık bir sayıyı üstel biçiminden dikdörtgen biçimine dönüştürmenin bir yolu. Daha sonra aralarındaki ilişki, Üssel, Kutupsal ve Dikdörtgen biçiminde bir karmaşık sayı tanımlarken verilir.
Karmaşık Sayı Formları

Fazör Gösterimi
Şimdiye kadar, karmaşık düzlemde bir noktayı tanımlamak için karmaşık sayıları kullanarak dönen bir vektörü veya durağan bir vektörü temsil etmenin farklı yollarını inceledik. Fazör gösterimi, verilen sinüzoidal dalga formunun genliğine ve faz açısına sahip tek bir karmaşık sayı oluşturma işlemidir.
Daha sonra bazen adlandırıldığı gibi fazör gösterimi veya fazör dönüşümü, sinüsoidal fonksiyonun gerçek kısmını aktarır: A (t) = A m cos(ωt ± Φ) zaman alanından, aynı zamanda frekans alanı olarak da adlandırılan karmaşık sayı alanına . Örneğin:
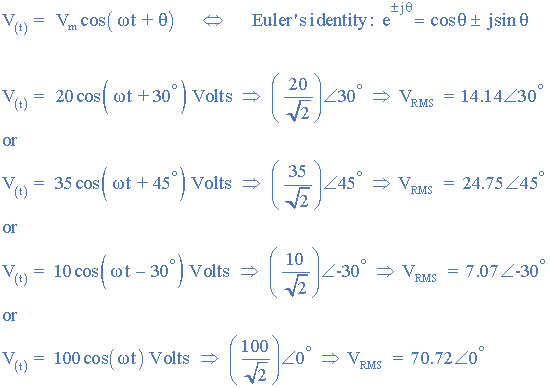
Lütfen √ 2’nin maksimum genliği radyan cinsinden verilen faz açısı ( ω ) ile efektif veya RMS değerine dönüştürdüğünü unutmayın.
Karmaşık Sayıların Özeti
Ardından, Karmaşık Sayılar ve elektrik mühendisliğinde karmaşık sayıların kullanımı hakkındaki bu öğreticiyi özetlemek için.
- Karmaşık Sayılar, bir gerçek sayı ve bir sanal sayı olmak üzere iki farklı sayıdan oluşur.
- Sanal sayılar j-operatörü kullanılarak gerçek sayıdan ayırt edilir.
- Önünde ” j ” harfi bulunan bir sayı , onu karmaşık düzlemde hayali bir sayı olarak tanımlar.
- Tanım olarak, j-operatörü j ≡ √ -1
- Hayali sayılar, gerçek sayılarla aynı şekilde toplanabilir, çıkarılabilir, çarpılabilir ve bölünebilir.
- “j”nin ” j” ile çarpımı j 2 = -1 verir
- Dikdörtgen Formda karmaşık bir sayı, karmaşık düzlemde uzayda bir nokta ile temsil edilir.
- Kutupsal Formda karmaşık bir sayı, uzunluğu genlik olan bir çizgi ve faz açısı ile temsil edilir.
- Üstel Formda karmaşık bir sayı, doğal logaritmanın tabanını kullanan bir çizgi ve karşılık gelen açı ile temsil edilir.
- Karmaşık bir sayı üç yoldan biriyle temsil edilebilir:
- Z = x + jy » Dikdörtgen Form
- Z = A ∠Φ » Kutupsal Form
- Z = A e jΦ » Üstel Form
- Euler’in kimliği, Karmaşık Sayıları üstel biçimden dikdörtgen biçime dönüştürmek için kullanılabilir.
Bunu içeren önceki derslerde, sinüzoidal dalga biçimlerini temsil etmek için fazörleri kullanabileceğimizi ve bunların genliği ve faz açısının karmaşık bir sayı biçiminde yazılabileceğini gördük. Ayrıca toplama, çıkarma, çarpma ve bölme dahil olmak üzere her bir karmaşık sayı cebir formu arasındaki dönüşüm ile Karmaşık Sayıların dikdörtgen, kutupsal veya üstel biçimde sunulabileceğini gördük .
AC serisi devrelerdeki fazör ilişkisi ile ilgili sonraki birkaç derste, bazı yaygın pasif devre bileşenlerinin empedansına bakacağız ve hem bileşenden akan akım hem de AC’den başlayarak ona uygulanan voltaj için fazör diyagramlarını çizeceğiz.
